Laboratory 5: Gesture RC Car
Laboratory Description
I2C sensors are used to further enhance the control developed in Lab 4. A remotely wired compass module is used to directly control the car with hand movements instead of through rotation of potentiometers, among other features.
Laboratory Goals
This laboratory is designed to further a student’s understanding of:
Using digital sensors to provide feedback,
Implementing and tuning PID control routines,
Preparation
Students should complete Lab 4 and Activity 14 prior to starting the laboratory.
Hardware and Tools
TI-RSLK Robotic Car
One CMPS12 Electronic Compass
One SRF08 Ultrasonic Ranger
Description
The speed and turning control inputs as implemented in Lab 4 provided for a direct calculation of the desired straight line and differential turn speeds using potetiometers. This lab introduces digital sensor(s) to provide similar control inputs; however, the sensor(s) are used to determine the cars response to external variable stimuli, as opposed to direct user manipulation. In this case however, the stimuli are still provided through user manipulation.
Instead of having the CMPS12 module mounted on the RSLK, it is instead mounted on a hand-held breadboard, akin to the mounting of the potentiometers for Lab 4. In one instance (Part A), the tilting of the breadboard completely controls the movement of the car: tilting the breadboard forwards and backwards (known as “pitch”) will cause the car to speed up and slow down, respectively. Tilting the breadboard left and right (known as “roll”) will cause the car to turn left and right, respectively. In another instance (Part B), rotation of the breadboard on the horizontal plane (known as “yaw”, measured directly as compass angle) is used to indicate the desired [relative] direction to car should turn towards, with pitch still controling car speed. Part C will entail…[TBD].
While the pitch speed control (tipping the sensor forward/back) corresponds nicely with the previously implemented potentiometer speed control of Lab 4, as does roll-based turning control (tilting sensor left/right); the compass-based turning control requires the car to achieve a specific heading. To accomplish this, a PD control scheme will be implemented. Note that the wheel speed Integral control routine from Lab 4 should be left unmodified.
The desired turning functionality (Part A versus Part B) is selectable via a slide switch wired on the car’s breadboard.
Part A:
Warning
There is an issue with the I2C protocol support between the CMPS12 and the MSP432P401R; where it does not seem to be possible to read only a single byte. Therefore, always read at least two bytes of data from the CMPS12. In cases where you only want to read a single register, use that as the start register and request two bytes to be read, ignoring the second read byte.
Circuit:
Using the same long wires used in Lab 4 and the I2C circuit from Lab 5, build the required hardware: the CMPS12 is to be mounted on the remote breadboard and connected to the I2C bus, with pull-up resistors mounted on the RSLK breadboard. There is no CMPS12 sensor on the car. Further: add a slide swith to either the car or remote breadboard (remote connection would imply another wire) and connect to a GPIO pin, configured as an input. This slide switch will be used in Part B.
Program:
Copy and modify your completed Lab 4 to remove the ADC and potentiometer dependencies and directly replace with measurements of the pitch and roll CMPS12 registers (see Electronic Compass, ADDR: 0x60 and CMPS12 Datasheet), where the compass is read using the same I2C module and functionality from the previous activity. Specifically, the program should read the pitch and roll register measurements and convert them both into desired speed, \(v_d\) and differential speed, \(\Delta v\) respectively. Your math from Lab 4 will need to be adjusted to account for the different values returned by the CMPS12.
Note
Remember that the maximum \(\Delta v\), \(\Delta v_{max}\), was a constant from Lab 4. This same constant should be used again.
Both the pitch and roll measurements should behave with the same type of response as from Lab 4, specifically:
The speed control should have the car stop if the desired speed is less than \(10\%\) duty cycle and should be limited to a maximum duty cycle of \(50\%\).
The turning control should have the car drive straight if the roll is near \(0^\circ\) (e.g., roll is within \(\pm 10\%\)) and should linear decrease/increase from \(\Delta v = 0\) to \(\Delta v = \pm \Delta v_{max}\) at some maximum tilt (e.g., roll is \(\pm 60^\circ\)).
It is up to the groups to determine a reasonable conversion between pitch angle and desired speed.
Checkoff
Demonstrate that the CMPS12 control implementation works well. Printing of suggested values above may be requested.
Angle-Based Turn Control
The angle-based turn control for Part B of this lab assumes the same method to turn control used previously, where the desired speed is manipulated with a differential speed between them that causes a rotation:
where \(v_d\) is the desired speed, \(v_l\) is the desired left wheel speed, \(v_r\) is the desired right wheel speed, and \(\Delta v\) is the steering control speed difference used to turn the car. As opposed to potentiometer or roll-based inputs however, the value for \(\Delta v\) is now calculated from the difference between a desired heading and the relative measured heading using a proportional and derivative control scheme:
Steering control system
Continuous control equation:
Discretized control equation:
where \(k_P^h\) is the steering proportional gain constant, \(k_D^h\) is the steering derivative gain constant, and \(\epsilon_h\) is the heading error.
Calculation of the heading error is not simply the difference between the desired heading, \(h_d\) (measured from hand-held CMPS12), and the relative measured heading, \(h_{rm}\) (calculated via encoders measurements):
as heading is a periodic function and is not necessarily linear; namely, the value for heading goes from \(0^\circ\) to \(359^\circ\) and then back to \(0^\circ\). This may result in erroneously large values for \(\epsilon_h\). For example, if \(h_d = 330^\circ\) and \(h_m = 60^\circ\) the direct calculation leads to \(\epsilon_h = 270^\circ\), which would cause the car to turn in the wrong direction towards the desired heading; that is, the long way. Of course, any angle in degrees is equivalent to itself \(\pm 360^\circ\), which may be used to correct the calculated \(\epsilon_h\) to determine the shortest direction to turn to reach the desired heading (three lefts make a right!). Applying to the previous example, the correct error would be \(\epsilon_h = 270^\circ - 360^\circ = -90^\circ\). It is necessary to always minimize the absolute value of \(\epsilon_h\). Since the value of the error may only be changed through \(\pm 360^\circ\), then the absolute value of the error must be bounded by half of that value: \(\left|\epsilon_h\right| \leq 180^\circ\), leading to the pseudocode:
heading error = desired_heading - measured_heading
If heading_error > 180 degrees
Subtract 360 degrees from the heading_error
If heading_error < -180 degrees
Add 360 degrees to the heading_error
...
continue control scheme
This is known as “wrapping” the angle to the \([-180^\circ,180^\circ]\) domain. Note that this should only be done with the calculated error, not the individual values for \(h_d\) and \(h_{rm}\)!
Similarly, the derivative of the error will suffer from the same when the error wraps around the \(\pm 180^\circ\) boundary in subsequent samples. However, this case only occurs when the car has a significant error, which is not generally expected when the program is operating correctly. Therefore, correction of the derivative error is neglected.
Calculation of Car Angle From Encoders
In this lab, we use the encoders to calculate the relative rotation of the car from an initial starting point (\(0^\circ\)), hence we refer to this measurement as a relative measured heading since an assumed starting point of \(0^\circ\) does not necessarily correspond to a compass direction and only depends on how the car was oriented when initialized.
To calculate the change in angle, we revisit calculations from Measuring Turn Angle from Lab 3; however, we improve these calculations by considering the case where the car can also be driving forward or backwards and not spinning in place. Further, we also assume that when viewing the RSLK movements in small segments, any driven curve can be represented as a circular arc:
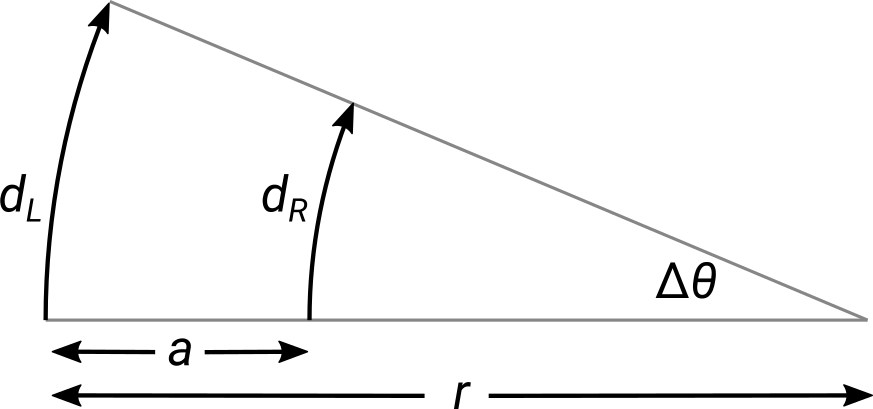
Turn angle geometry
In this figure: both the left wheel and right wheel are shown to travel some distance forward, \(d_L\) and \(d_R\) respectively, the wheels are separated by a length, \(a\) (the RSLK width). Due to the difference between \(d_L\) and \(d_R\) the left wheel traces a circle of radius \(r\), the right wheel traces a circle of radius \(r-a\), and the RSLK turns with an angle change of \(\Delta\theta\). From this diagram, we can assemble the two equations:
Solving for \(r\) in the first equation, substituting into the second equation and solving for \(\Delta\theta\) gives the expression:
Of course, we can calculate both \(d_L\) and \(d_R\) from how many encoder events have occurred within the considered drive segment and the conversion is the same for each wheel. Therefore, we can modify this equation to instead be:
where \(n_L\) and \(n_R\) are the tracked number of encoder events for the considered segment and \(C\) is the conversion factor to convert between encoder counts and travel distance: \(d_L = C n_L\) (calculated in Lab 3).
Again, this calculation is only applicable for when the change in angle is recalculated often such that only small segments of the drive path are considered (or if the car is driving in a perfect circle). Therefore, to get the actual car orientation angle at time sample \(k\), \(h_{rm}(k)\), the \(\Delta \theta\) values for each drive segment from the start to sample \(k\) must be added together:
This is very similar to how the error sum for I control has been tracked! That is: for each instance where \(\Delta \theta\) is calculated, the calculated value is also added to \(h_{rm}\).
Again, note that this value for \(h_{rm}\) is not the true orientation of the RSLK but a relative orientation considering its initial orientation (that is, the orientation when it was turned on) as \(0^\circ\).
Finally, it should be understood that although the figure drawn shows that both wheels are traveling in the same direction it is not required for this math to be correct: one wheel may be traveling forward and the other in reverse and the calculations will still hold. This implies that the direction of the encoder counts (forward/backward) must be tracked in addition to the total number!. As such, encoder counts that occur when the wheel is travelling in reverse should considered “negative” counts, which subtract from the total number of counts.
Part B:
This part of the lab should be assembled in a specific order in order to verify pieces before assembly of the whole program.
Selection of Turn Control Method
Implement the slide switch control to be able to disable CMPS12 roll measurement based turn control. Switching of the slide switch at any time during program operation should cause the roll turn control to be activated or deactivated, depending on the switched state.
When the roll turn control is inactive, the angle-based turn control should be active (yet to be implemented). Verify the slide switch functionality works correctly by running the modified program. With the switch moved such that the roll measurement based turn control is active, the RSLK should act exactly as in Part A. With the roll measurement based turn control deactivated, the RSLK should only be capable of straight line driving forward and backwards at this point.
It is suggested to have a printf() statement added to each condition to indicate which state the program is in.
Calculate Relative Measured Heading
The next step is to generate the relative measured heading, \(h_{rm}\), as defined in the previous section. To do so, you must:
Modify the tracking of the total encoder events such that if the wheel is traveling in the forward direction, events are added to the total. If the wheel is traveling in the reverse direction, events are subtracted from the total. This may be done simply by tracking the state of the secondary encoders on each wheel (P5.2 for the left wheel and P5.0 for the right) as described in the Encoders lecture: if the value of P5.2 is low when a left encoder interrupt is triggered, the wheel is traveling in reverse whereas a high value would indicate the wheel is traveling in the forward direction (the directions indicated here may be flipped and incorrect. They should be fixed through testing, if necessary).
Calculate the values for \(\Delta \theta\) and \(h_{rm}\) each time the control loop runs.
After the calculation for \(\Delta \theta\): reset the encoder events counters such that they are only tracking the number of events between control loop iterations. This would determine the “drive path segment” considered, as discussed above. If a running total of encoder events is still desired, another variable may be used instead for the segment tracking.
The calculation above may be tested with the motors off: set the car on the bench and move it manually by hand while also printing out the calculated value of \(\theta\) after each control loop iteration. If the calculations are correct, the car should report fairly accurate orientation changes. Please be gentle when moving the car by hand: abrupt and strong movements wear the gear train clutch within the motor housing.
Note that the calculation of \(h_{rm}\) done here will be in radians!
Add Angle-Based Turn Control
Implement the angle-based turn control as described above. Since \(h_{rm}\) is calculated in radians, it must be converted to match the units of the CMPS12 heading measurement: tenths of degrees (0-3600).
This control should follow the pseudocode:
Calculate the heading error and "wrap" the error to -180 to 180 (or -1800 to 1800)
Calculate the differential speed using the PD control (equation given above)
Enforce maximumum limit on differential speed to 20 % duty cycle
Store the current heading error as previous heading error (for derivative control)
The enforced limit on differential speed as given in the pseudocode is necessary as without it the RSLK will spin much too quickly for the derivative control to be useful due to the slow iteration rate of the control routine (set as 100 ms per loop in Lab 4).
In addition to these additions, increase the iteration period of the control routine from 100 ms to 50 ms to further aid in the derivative control operation. Note that the since the CMPS12 updates at approximately 33.3 ms (estimated), it is not useful to reduce the control routine below this value as no new data to act on would be available. Because the routine is running faster, the error accumulation for the integral control will happen twice as fast; therefore, it is necessary to halve the integral gain constant, \(k_I\).
All other control specifications are carried over from Lab 4:
Quantity |
Value |
Notes |
|---|---|---|
Max |Diff Speed|, \(\Delta v_{max}\) |
20 % |
Set | \(\Delta v\) | to this if greater than |
Min |Speed|, \(v_{d,min}\) |
10 % |
Set |desired speed| to 0 if less than |
Max |Speed|, \(v_{d,max}\) |
50 % |
Set |desired speed| to this if greater than |
Min PWM DC % |
10 % |
Set compare value to this if less than |
Max PWM DC % |
90 % |
Set compare value to this if greater than |
Control Routine Period |
50 ms |
Tune the Turning PD Control
Finally, the proportional and derivative gain constants, \(k_P^h\) and \(k_D^h\), for the angle-based turn control must be tuned. To do so:
Assume a constant value for the desired heading, \(h_d\), instead of using the compass value measured from the CMPS12. Further, force the desired speed to be 0. This control should allow the car to spin in place without moving forward or reverse. A good starting value to assume for the desired heading is \(90^\circ\), or \(900^\frac{\circ}{10}\), but other values should be tested as well. Note that this suggested value implies a starting heading error of \(\epsilon_h=\left(900-0\right)=900\), since the RSLK will always start with a measured value of 0.
Tune the \(k_P^h\) and \(k_D^h\) using the same method as presented in Activity 13:
Starting with a small value, gradually increase \(k_P^h\) until the car quickly responds to the desired heading but oscillates about it. Do this with \(k_D^h = 0\).
Starting with a small value, gradually increase \(k_D^h\) such that the car still responds quickly to the desired heading but no longer oscillates (it may still overshoot, however). Note that if the car rotation speeds up with increasing \(k_D^h\), the sign of \(k_D^h\) is likely incorrect.
Important
You must be careful selecting initial “small” values for \(k_P\) and \(k_D\): in some cases, a value of “1” might be considered small but in others it may be too large. For this case, the heading control is using the heading error, \(\epsilon_h\), to produce a PWM duty cycle. As \(\epsilon_h\) is by default in tenths of degrees \({}^\frac{\circ}{10}\) (unit from sensor), it will be in the range \([-1800^\frac{\circ}{10},1800^\frac{\circ}{10}]\). A “small” error would still be a large number, e.g., \(-150^\frac{\circ}{10}\). Multiplying this error with \(k_P=1\) results in a desired duty cycle of \(-150 \%\)! By this, it is clear that \(k_P\) should be much smaller to start tuning, such as \(k_P = 0.01\).
While testing, ensure to print out applicable variables for debugging, such as the measured heading, the current error, and the proportional and derivative control contributions to the calculated differential speed.
When complete, allow both the \(h_d\) and desired speed to be set by the CMPS12.
Checkoff
With all components listed above completed, demonstrate the full functionality as described. Printing of suggested values above may be requested.
Part C: Measurement and Control Characterization
Measurements
This portion of the lab entails reporting on the measurement accuracy and control efficacy of the system from Part B. This reporting work is the replacement for the “final project” of this course.
Three distinct measurements and plots are requested for this:
Two measurements characterizing the effectiveness of the pitch speed control, both with and without \(k_I=0\) (wheel speed integral control off and on): Groups should first disable steering control for this step (enforce \(\Delta v=0\)) such that the car only drives forward and reverse. Set the program to print out three values each time the control routine iterates:
Desired speed
Left wheel measured speed
Right wheel measured speed
These measurements should be done with the RSLK on the ground and not supported by the foam block. This will cause inertia (weight) of the RSLK to have more of an effect on the response. Each measurement should be done over a span of time to allow for the car to accelerate from stop to constant-ish forward speed (quickly rotate CMPS12 down and hold at constant angle) and then to constant-ish reverse speed (rotate up and hold at constant angle) to simulate two step changes in desired speed.
Two measurements characterizing the effectiveness of the angle-based turn control, both with and without \(k_D^h=0\) (turning derivative control portion off and on): Groups should first disable pitch speed control for this step (enforce \(v_d=0\)) such that the car can only spin in place. Set the program to print out five values each time the control routine iterates:
Desired heading angle (from compass)
Relative measured heading angle (from encoders)
Desired differential speed
Left wheel measured speed
Right wheel measured speed
These measurements should be performed similar to the previous but instead the angle is being controlled instead of the speed.
One measurement characterizing the accuracy of the encoder heading angle calculation. For this measurement, the motors are to be set to off (as in initial testing in Part B). Affix the compass to the RSLK as opposed to remotely (can just clamp remote protoboard to RSLK protoboard if easier, clips will be available in classroom). For each iteration of the control loop (which isn’t technically doing anything), print out:
Measured heading from compass
Calculated heading from encoders
For this last measurement: the test should start with the RSLK being rotated in place to 90° or 180°, moved back to 0°, then moved in a random fashion (both moving forward and reverse while turning), ultimately returning to the initial 0° position (sensor and/or calculation do not necessarily have to indicate 0°).
Hint
For all measurements, it is suggested to print out all values for one sample point on one line, either separated by commas or spaces, such that when the data is imported into a program, it is easy to parse into columns or arrays.
The easiest way to extract the data from the terminal is to:
Clear the terminal before a measurement.
Run the measurement and then pause the code to stop printing.
Right click within the terminal and choose “Select All”
Copy the selected material (CTRL+C)
Paste the copied data to your target program/file.
This implies that a computer is connected to the RSLK during the measurement, so a long usb cable is necessary.
Alternatively, the data may be saved to long arrays and then printed onto a terminal connected after a measurement is completed. In this case, when connecting the car to the computer, do not start a new debug session as that would erase the data in memory, only connect the terminal.
Documentation
For each set of measurements (total of 5): Save all data to a spreadsheet or text file and import into a plotting program, such as Excel, Google Sheets, MATLAB, or any other applicable program. For each measurement plot all values saved, either on one or multiple axes (at minimum, one axes set per measurement set) such that the data is easy to read and all axes/lines are fully labelled, including with units.
Create a document containing all plots (sectioned appropriately). Each plot should have a description or title indicating which measurement it was generated from. In addition, add a short paragraph for each measurement set interpreting the results as shown in the figures: for example, if the measurements show that the pitch speed control did not stabilize (e.g., didn’t reach steady state) or had significant steady state error, indicate as such and attempt to explain why. Make sure to indicate the differences between when wheel speed integral control is turned off and on. Similarly, indicate differences between when turning derivative control is turned off and on.
Submit your generated “report” document to the “Lab 5C Documentation” Gradescope assignment.
Rubric
- Each of the 5 measurements sets will be graded out of three points:
3/3: Plots and description aptly describe what is going on with the system. Plots are sufficiently labeled and are produced using data as required. One or two minor errors are acceptable for full credit.
2/3: Plots and description are fairly good but are lacking in one major aspect or several smaller aspects. For example, plots are not complete (missing a line) or not fully labeled (e.g., no units). Descriptions might describe plots well but do not interpret them quite correctly.
1/3: Plots and description exist and generally follow the guidance above, however, maybe aspects are not correct.
0/3: Plots and description do not exist or do exist but are not interpretable, do not follow the instructions, other other serious issues.